光速の背景　　47
 次ページ
第２章　疑うべき学説
ある。それには、Ｋ´時計が合っている軸（空間軸）がＫ系の空間軸とは異なり、「光線が軌跡の両端と交わる２点Ａ´、Ｂ´を結ぶ斜めの線であればよい」と喜ぶ。これをχ´軸――(だがこれが物指だとすると、最初の約束を破って時間をまたぐ仮想の線であって、空間を示す量ではない)―― と呼ぶ。ＫとＫ´との同時刻の定義が異なる、と説明される。相互にはなぜか、αとβを含んだ式（表２）で表わされ、ｔ´は表計算④式のようになる。
　また、表３のような計算でも⑤式が求まる。これと比較してαが決まり、⑥式を得る。
図６

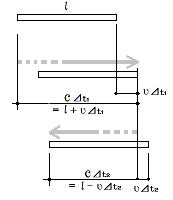
長さについては、常識論からはＫ系で光の往きに要する走行距離は光速ｃ×往き時間⊿ｔ１として表４での計算のように決まり、戻りは光速ｃ×帰り時間ｃ⊿ｔ２として決まるはずで、往復ではその和、同表⑨式となる。
　相対論によれば運動中の棒に乗って見ている棒の長さＬの２倍を光速ｃで除したものが、運動系での時間である(表４)。すなわち、Ｋ´時計で測ったときには、往復して光が左端に戻るのに要する時間は片道の倍で⊿ｔ´＝２Ｌ／ｃである。これは表２の⑤式を加味すれば、表４のようにして⑩式ｌ＝Lへ導く。これはＫ系の観測者から見て運動方向の長さがの割合で短縮していることを示している、とする。
　χ´についてはなぜか表計算のようにおいて⑪式を得るから、Ｋ´とＫとの位置座標関係はこの式で結ばれる。これとさっきの⑥式と合わせてローレンツ変換と呼ばれている。

　　（相対論）――時間について

ＫとＫ´の時刻の定義が異なり、相互にはct´＝αct＋βχの関係にあり、ｔ´＝0でct＝－(β/α)χとなる。その傾きはυ/ｃに等しく、－(β/α) ＝υ/ｃで１個の係数αが残り
　t´＝α（ｔ－υχ/ｃ2）　　(χ=υt)
　　　　　　　　　　　　……④
となる。また表３の計算からも得られるように
　t′＝ t …………⑤
　これと比較してα＝1/と決まり、
　 t´＝（ｔ－υχ/ｃ2）／ 　　　　　　　　　　　　　　　　　　　……⑥
（だが、χ/ｔはυであるから、この式は
　ｔ[1－υ2/ｃ2]／
　＝ｔ
となって　⑤式と同じものだ）


　　　　　　　　　表２　　　表３		 　　　（相対論）――光速不変

相対論では光速不変を前提に

往き

 c t　＋υt

＝

c

……⑦
t

帰り

 c t　－υt

＝

c

……⑧
t

だとする。両式を乗じてみると
(ct＋υt)( ct－υt)／t´2＝c2
　これは

(t´)2

＝

 (c t)2　－　(υt)2

 
c 2



　となって、時間t´は
　t′＝ｔ＝βt　…⑤
　　　(＝βとおいた)
　と短縮する。したがってυで走行中のアーム長さはct´＝cβtつまり静止長さL=ctに対してβの率で縮んでいると結論する。　　　　　　
  47
 次ページ