嘋
傊偺
媈栤
![]() 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂![]()
仚丂丂仚丂摿庩憡懳榑嘋傊偺媈媊丂丂仚丂丂仚
3-俈幃偼偳偺傛偆偵偟偰摫偐傟偨偺偩傠偆偐丅傕偆傂偲偮栠傞偑丄3-5幃偼3-4幃偺曄宍偱摨偠傕偺偱偁傞丅擮偺偨傔傗偭偰傒傛偆丅傑偢3-4幃偺嵍曈偡傋偰傪塃曈傊堏崁偟偰偐傜斀揮偡傞偲
丂![]() 乧乧嘋
乧乧嘋
偲側傝丄妵屖偺側偐傪惍棟偡傟偽3-5幃傪摼傞丅偙傟傜偼3-3幃偐傜冊(亴)仺侽偺嬌尷丄偡側傢偪嵗昗尨揰偵偍偗傞冄偲倲偺娭學幃偱偁傞傛偆偩丅偟偐偟丄偙偺3-5幃偱偁傞
丂丂![]() 丂乧乧乧乧乧乧丂嘍
丂乧乧乧乧乧乧丂嘍
偼慜偵傕弎傋偨傛偆偵丄偁傗偟偄丅傕偟偙傟偑惓偟偄偲偟偰冊(亴)偱愊暘偟偰傒傞偲丄
丂丂![]()
偲側傞丅愊暘掕悢俠偼冊(亴)亖侽偺偲偒乮尨揰偵堦抳偟偰偄傞偲偒乯冄亖倲偱偁傞偐傜倲亄侽亄俠亖侽偱俠亖丂乚倲偲寛傑傞乮偙傟傜偺冄傗倲偼乽帪崗乿偱偁傞乯丅偡傞偲
丂丂![]() 丂丂
丂丂
偲側傞偐傜丄冄埲奜傪堏崁偡傞偙偲偵傛傝
丂丂![]() 乧乧乧乧乧乧乧乧乧嘐
乧乧乧乧乧乧乧乧乧嘐
傪摼傞偑丄偙傟偼3-7幃偵堦抳偣偢丄![]() 偑梋暘偵擖傞丅3-7幃偺倎偼偺偪偵倎亖侾偲摼偰偄傞偑丄嘐幃偑偙傟偵堦抳偡傞偵偼
偑梋暘偵擖傞丅3-7幃偺倎偼偺偪偵倎亖侾偲摼偰偄傞偑丄嘐幃偑偙傟偵堦抳偡傞偵偼![]() 亖侾偱側偗傟偽側傜側偄丅
亖侾偱側偗傟偽側傜側偄丅
丂偲偙傠偑丄偙偺偁偲偵冄亖冇乮円乯兝乮倲丂乚丂円冊乛俀們乯乮3-13幃乯偑摫偐傟傞丅偡傞偲丄偙傟傪倲偱曃旝暘偟偰傒傞偲
佪冄乛佪倲亖冇乮円乯兝偲側傝丄偺偪偵冇乮円乯亖侾丄乮兝亞侾乯偲寛傑傞偲側傟偽丄円亖侽偱側偄偐偓傝![]() 亖侾偵偼側傜側偄丅偟偨偑偭偰嘐幃偺尦偱偁傞嘍幃偼憡懳榑偺慜採偐傜柕弬偡傞丅偮傑傝丄傢傟傢傟偵晄柧偱偁偭偨偝偒傎偳偺3-3幃偐傜3-4幃傊偺偁偄偩偵旘桇偑偁傞偺偱偼側偄偐丅3-4幃偐傜岻傒偵3-7幃傪摫偔偑丄偺偪偵摼傜傟傞傕偺偲柕弬偟偰偟傑偭偰偄傞傢偗偩丅
亖侾偵偼側傜側偄丅偟偨偑偭偰嘐幃偺尦偱偁傞嘍幃偼憡懳榑偺慜採偐傜柕弬偡傞丅偮傑傝丄傢傟傢傟偵晄柧偱偁偭偨偝偒傎偳偺3-3幃偐傜3-4幃傊偺偁偄偩偵旘桇偑偁傞偺偱偼側偄偐丅3-4幃偐傜岻傒偵3-7幃傪摫偔偑丄偺偪偵摼傜傟傞傕偺偲柕弬偟偰偟傑偭偰偄傞傢偗偩丅
丂偡傞偲3-俈幃偼偳偙偐傜摼傜傟偨傕偺偩傠偆偐丅3-3幃偵偁傞冊(亴)乛乮們丂乚円乯偼丂俷(亴)偐傜俹(侽)傊偺墲偺帪娫丄冊(亴)乛乮們亄円乯偼暅偺帪娫偱偁傞丅偙偺嵎傪偲傟偽墲暅偺帪娫嵎偲側傝丄偦偺敿暘偱曅摴偁偨傝偺抶傟帪娫偵側傞偲峫偊偨偺偩傠偆偐丅帪崗倲乮俲嵗昗偱偺帪崗乯偵懳偟丄倠嵗昗偱偼倲傛傝偝偭偒偺抶傟偩偗彮側偄帪崗偵側傞丅偦偺寁嶼傪偡傞偲丄冊(亴)乛乮們丂乚円乯偲冊(亴)乛乮們亄円乯偺嵎偼![]() 偲側傝丄偦偺敿暘傪倲偐傜堷偔偲偨偟偐偵3-7幃偲側傞丅摢偺倎偼偝傜偵壗偐偺尨場偱怢弅偡傞偐傕偟傟側偄偲峫偊偰晅偗偨傕偺偐丄偁傞偄偼撉幰傪尪榝偡傞偨傔偺傕偺偐傕偟傟側偄丅偁偲偱倎亖侾偲側傞丅
偲側傝丄偦偺敿暘傪倲偐傜堷偔偲偨偟偐偵3-7幃偲側傞丅摢偺倎偼偝傜偵壗偐偺尨場偱怢弅偡傞偐傕偟傟側偄偲峫偊偰晅偗偨傕偺偐丄偁傞偄偼撉幰傪尪榝偡傞偨傔偺傕偺偐傕偟傟側偄丅偁偲偱倎亖侾偲側傞丅
丂忋偺傛偆側峫偊偩偲偡傞偲![]() 偼乽帪娫乿偲偄偆偙偲偵側傞丅倲偼帪崗側偺偐丄帪娫偐丠丂倲偑帪崗側傜冄偼乽帪崗乿丄帪娫側傜乽帪娫乿偺傢偗偵側傞丅
偼乽帪娫乿偲偄偆偙偲偵側傞丅倲偼帪崗側偺偐丄帪娫偐丠丂倲偑帪崗側傜冄偼乽帪崗乿丄帪娫側傜乽帪娫乿偺傢偗偵側傞丅
丂丂丂兲亖們冄
偲偄偆幃偵揔梡偡傞傕偺偱偁傞偲偡傞偲丄偙偺冄偼乽帪娫乿偱側偗傟偽側傜側偄丅偡傞偲倲偼帪娫偱側偗傟偽側傜側偄丅側偵傪偟偰偄傞帪娫偐丠丂3-3幃偼乽倠宯偺冄傪弌敪帪冄侽偵偮偄偰俲宯偱倲乿偲偡傟偽倲偼帪崗偲偄偆偙偲偵側傞丅偦偺棳傟偐傜棃傞3-7幃偺倲偼帪崗偱偁傞丅倲偑帪崗偱偁傟偽3-8幃偼惉傝棫偨側偄丅懍偝偵帪崗傪忔偠偰傕嫍棧偵偼側傜側偄偐傜偱偁傞丅
丂偦偙偱偙偺倲傊3-9幃偺乽帪娫乿偲偟偰偺倲傪擖傟傞丅偟偐偟偙偺倲偼冊(亴)偺嫍棧傪丄偙偙偱偼岝偺懍搙傪們丂乚円乮斵偼岝懍傪偳偺嵗昗偱傕們偲偟偨偼偢偩偑乯偲偟偰丄岝偑憱傝偒傞帪娫偲偟偨冊(亴)亖乮們丂乚円乯倲偺倲偱偁傞丅偙偺倲偼弌敪帪偐傜曄壔偟偰偄偔帪崗偱偼側偔丄憱峴乽帪娫乿偱偁傞偲偟偰3-8幃偵擖傟傞丅偙傫側婥傑偖傟側偙偲傪偟偰偼側傜側偄丅
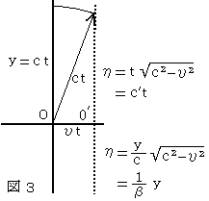 們亴偼傏偔傜偺岝偺憡懳懍搙偱偁傞 |
丂丂丂丂丂 | 側偍丄乽岝偼忢偵偙傟傜偺幉偵増偭偰懍搙 |
幃偺桿摫傪傕偆偡偙偟尒偰偍偙偆丅3-4幃偑偍偐偟偄偙偲偼慜偵弎傋偨丅3-7幃乮帪崗乯傪梡偄偰嵗昗3-8幃偑摼傜傟偰偄傞丅偦偺忋偺兲亖們冄偵拲堄偟傛偆丅偙偺冄偼柧傜偐偵乽帪娫乿偱偁傞丅偮傑傝3-8幃偵擖傞傕偺偼乽帪娫乿偱側偗傟偽側傜側偄丅偦偙傊乽帪崗乿乮3-7幃乯傪曻傝崬傫偱偄傞両丂偙偆偟偰帪崗倲偼帪娫倲偵偡傝偐偊傜傟偨丅偦傟偐傜丄偙偺幃偵乽倠宯偺弌敪揰偵懳偟偰丄懍搙乮們丂乚円乯偱摦偄偰偄傞乮偙傟偼憡懳懍搙偱偁傞偲尵偭偨偺偲摨偠偱丄帩榑傪扞偵忋偘偰偄傞乯乿偲偟偰3-9幃傪擖傟偰3-10幃傪摼偰偄傞丅
丂傑偨丄3-13幃偺冄偵娷傓倲偼3-9幃偺倲偲偼傑偭偨偔柍娭學偺倲偱偁傞偙偲傪擮摢偵抲偔昁梫偑偁傞丅偙偺冄偼媈榝偺3-7幃乮帪崗乯偵冊(亴)亖冊丂乚円倲乮偙偺倲偼乽帪娫乿偱丄嵗昗塣摦偵偐偐傢傞倲乯傪戙擖偡傟偽丄冄亖倎俀兝乮倲丂乚円冊乛們(俀)乯偲偟偰摼傜傟傞丅偙傟傕曄偱偁傞丅偪傖傫偲偟偨壢妛幰偵棟夝崲擄側偺偼摉傝慜偲偄偆傕偺偩丅
丂師偺幃偼偍偦傜偔儅僀働儖僜儞傪堄幆偟偰倷亖倲
丂偙偺幃偲冊(亴)亖侽傪3-11幃偵擖傟偰3-12幃偑偱偒偰偄傞丅偟偐偟丄冊(亴)偵懳偟偰偦偺抣傪偍偒偐偊傞偲3-13幃偵側傞偲偄偆偑丄側偤偙偆側傞偺偐巹偵偼暘傜側偄丅偍偦傜偔兣丄兡偵偮偄偰丄帩榑偺岝懍搙晄曄偐傜偡傟偽倷亖兣偱側偗傟偽側傜偢丄偦偺偨傔偺廋惓傪偟偨偺偱偁傠偆丅偦傟偲傕丄偁偲偺曽偱弌傞4-2幃偐傜僼傿乕僪僶僢僋偟偰柍棟傗傝挷惍偟偨傕偺偐偲傕巚傢傟傞丅偦傟偐傜丄3-16幃偼丄偙偆偼側傜側偄偺偩偑乧丅
丂偲偵偐偔丄
丂丂丂冄亖倎兝(俀)乮倲丂乚円冊乛們(俀)乯
丂丂丂兲亖倎兝(俀)乮冊丂乚円倲乯
丂丂丂兣亖倎兝倷
丂丂丂兡亖倎兝倸丂丂丂丂丂丂丂丂丂丂丂乧乧乧乧乧乧埲忋3乚12
偱偁傞丅偙偺幃偐傜師偵丄冊(亴)偵懳偟偰偳偺抣傪丄偁傞偄偼冊(亴)傪偳偺傛偆偵抲偒姺偊傞傕偺偐丄兝偑堦偮偢偮奜偝傟偨3-13幃偵側傞偲偟偰偄傞丅偄傠偄傠傗偭偰傒偨偑丄傗偼傝偳偆傕暘傜側偄丅3-12幃偵偮偄偰偼偝偭偒弎傋偨傛偆偵丄恾俁偺偲偍傝倷偲兣偑擖傟懼傢傞偺偑惓偟偔丄兣亖倎乮侾乛兝乯倷丄摨條偵兡亖倎乮侾乛兝乯倸偲側傞傋偒偱偁傠偆丅偦偺徹嫆偵3-8幃偺忋丄兲亖們冄偐傜暘傞傛偆偵丄兲偼斵偺棟榑偵傛傟偽帪娫冄偺抁弅暘乮3-7幃偐傜冄亝倲偱偁傞乯偩偗彫偝偄偼偢偑丄3-12幃偺兲偼俀兝乮兝亞侾乯偵傛偭偰媡偵戝偒偔側偭偰偄傞丅偩偐傜3-12幃偼偦傟偧傟侾乛俀兝丄侾乛兝偲偡傞忦審偱丄岝偺嵗昗偑惷巭宯俲偵惷巭偟丄倠宯偑懍搙円偱冊幉忋偺惓偺懁傊塣摦偟偰偄傞偲偡傟偽丄倎亖侾偲偟偰偙傟傜偺兣丄兡偼惓偟偄丅恾俁傪嶲徠偟側偑傜兣偵偮偄偰尵偊偽
丂丂丂兣亖
偱偁傞丅椉嵗昗偺倷嵗昗偑偲傕偵尨揰俷偐傜倷曽岦偵摨偠倲昩娫偵岝偑恑傓嫍棧偩偲偡傟偽惓偟偄丅嵗昗曄姺榑偲偟偰悢抣傜偼岝懍偲偄偆尰幚偺摴嬶傪巊偊偽丄側傞傎偳偦偺傛偆偵側傞丅
丂偙傟偵懳偟丄偳偆偡傟偽偙偆側傞偺偐暘傜側偐偭偨3-13幃偼兣偲兡偵偮偄偰偼悢妛偲偟偰寢壥揑偵惓偟偄丅兲偵偮偄偰偼兝亖侾偱偁傟偽惓偟偄偺偩偑丄椉嵗昗偱偺帪娫偑堘偆偲偄偆慜採偩偐傜丄偡偙偟柺搢側幃偵側偭偰偄傞丅
丂偡側傢偪丄乽岝乿偲偄偆尰幚偺尰徾傪夘嵼偝偣側偗傟偽丄晛捠偺僈儕儗僆曄姺乮3-13幃偺倷丆倸嵗昗乯偲側偭偰丄壗傕栤戣偼側偄丅憡懳榑偱偼兲偵兝偺擖偭偨傕偺傪梡偄偰偙偺愭傊恑傔傞丅偮傑傝冊幉偵偮偄偰偼塣摦偵傛傞帪娫偺抁弅偑偁傞傕偺偲偟偰恑傔傞偑丄偦偆偩偲偡傟偽嵗昗娫憡懳懍搙偺惗偠側偄倷丆倸幉偵偮偄偰傕3-12幃乮偨偩偟兝偨偪偼媡悢乯偺傛偆偵抁弅傪尒傞傋偒偲偙傠丄傑偭偨偔抁弅偼側偄傕偺偲偟偰偄傞丅3-13幃偼嬝偑捠偭偰偄側偄丅
丂3-12幃側傜傛偄偐偲偄偊偽丄岝偺棙梡偲偟偰嬝偼捠傞偑丄尰幚偵偼岝偺嵗昗偑俲宯偵惷巭偟偰偄傞傕偺偐偳偆偐妋擣偡傞偙偲偼晄壜擻偱丄壦嬻偺榖偵側傞丅乽岝乿偲偄偆尰幚偺摴嬶傪梡偄側偑傜丄幚尰晄壜擻側壦嬻偺棟榑偵側傞丅
丂傾僀儞僔儏僞僀儞偼偙偺愭丄屻幰偺3-13幃偺寢榑偱偁傞3-17幃傪嵦傞傜偟偄偑丄偙傟傜偺幃偵偼柕弬偺偁傞偙偲傪偝偭偒尒偨丅
丂偁偲偡偙偟偩偗尨暥傪撉傕偆丅偦傟偱摿庩憡懳惈棟榑偺梫揰傪傎傏偙偊傞丅丂
丂尨暥偺懕偒傊