金食い坊やがひょっこり眼を覚まして、わけの分からぬうわ言を言ったと思ったら、また寝入ってしまった。おかげでわたしも、暑くって眠れぬ、夏の夜だ。

ほんとうに、モノの最初はいかに存在したのか？　たしかにこれは、最も興味をそそる謎だ。ぼくらの世代にそれを知るのは無理かもしれない。幸い、わたしは暇になって、もう長いこと、考えることぐらいしかない。かくてディオゲネスのように、日がな思考の樽を転がしていたものだから、謎の奥地に近いところまで来ているような気もする。
　しかし、すべての推理の初めは、物理の最も基本的な“自然法則”に基づかなければならない。勝手な妄想を持ち込んではだめだ。物理に拠るべしだ。そこでたいていわたしは、自分が最も初期に学んだ物理から入ることにしている。そしてそこから、理路整然と発展させようとする。
　いま最大のテーマは、

――それこそが物質の誕生、宇宙の始まりの謎なのだが――だ。
　まさかヒッグス粒子とかいう素粒子が突如現れて、他のあらゆる素粒子仲間に質量をふり与えたなんて話を、いくらなんでも拝受するわけにはいかない。われわれが真面目な学習によって今までに知ったことは、万有引力の場(重力場)は質量がつくっている。磁場は磁荷がつくっていて、電場は電荷がつくっている。電線を流れる電流は、その周りに磁界を発生させる。図１のようである。

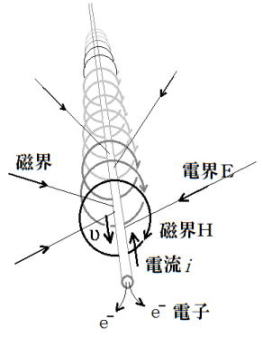図1

そして理科実験で、たしかにそうであることを確かめた。われわれの物理学では、陽電気の流れる向きを電流の向きとした。これは理論を進めるための単なる約束事だ。すると電流の向きは、通常、負電荷をもつ電子が流れる向きとちょうど反対になる。

1.観察する

図1の円輪の束たばの中心を貫通している細いダブル線は、太さを表現した電線で、手前の小さな丸は、その仮想断面を示す。実際には電池までつながっている。この断面から電子が飛び出る向きに流れているものとすると、電流は電線を向こうへ向かって流れることになる。この約束のために、いつもややこしくなって仕方がない。右ネジ(市販のほとんどは右ネジ)をこの向きに進めるためにネジを回す回転方向は、手前から見て時計回りだ。これを「右回り」と呼ぶことにする。
　学校ではネジを前方へ(電流の向きに)進めるように回す向きに磁界が生じると教わった。この磁界の向きは、Ｎ極からＳ極へ向けるのをもって「磁界の向き」と決める。磁界は線状に出るわけではないが、人の頭ではそのようにイメージして進める。
　また磁界は、Ｎ極から出発してＳ極のほうへ伸びて行く、というものではない。図で、導線の中に行列している電子はそれぞれ電界を持ち、物理学上の約束によれば、それらの電界はぜんぶ空間から導線内の電子へ向かっている。電子は負電荷を持つからである。細い電線へ向かう無数の電界(電気力線)は、ちょうど試験管ブラシのように、電線に向かって集まるだろう。図２の写真のようである。

ブラシの木　　　　　　図2

これは「ブラシの木」という植物の花である。導線に電流を流すことは、このブラシの木が軸線にそって前後に動くようなものであり、その毛全体がわさわさと動いて、そのため船のスクリューのように周辺のなにかを動かし、実際に渦を生じさせるのだが、その渦が磁界である、ということになる。このようにイメージしたら間違いないだろう。自然界のつくりとは、なんと想像力豊かなものであることか！

　図１では円輪の束の矢印の向きに、まるく磁界が生じていることを示す。図では各断面に１つずつの円しか描いてないが、実際には樹木の年輪のように無数の同心円状の磁界が取り巻いている。自然が実際にとっている電流や電子の動きと磁界の関係は図のようになっている。
　「ああ、そうですか、分かりました」では進歩がない。正直、まだわたしには何も分かっていない。いったい、電子の動きが、電子が触れてもいない空間に、なぜ磁界を生じさせるのか、とてもとても謎だ。こんなに謎なのに、親愛なる友よ、なぜ貴君はやすらかに眠ることができるんだ！

しかし、素直にその事実を認めた上で、つぎにわたしがすることはその事実に関する分析だ。それはこんな風になっている。

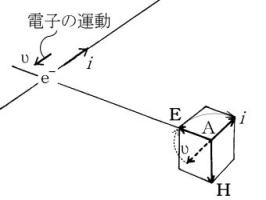図３

図３では空間を電子(負電荷を持つ)が図の向きに直線運動している。電子は舗装された、電線という道路を軽快に走る。図中の細い十字は、われわれの頭の中に描く仮想の座標(電線に対して静止している)で、この上で電子の運動の向きと反対に電流が起きているとイメージする。つまり、電場を伴った電子が電場とともにυの速度で運動している。すると、さっき知ったことはこう言い直すことができる。

空間のある点Ａで考えると、Ａ点の周りでベクトルＥからベクトルｉ　の向きにネジを回わせばネジが進む向き (図では下向き)に、磁場Ｈが生じると分析してよいだろう。図１では磁界Ｈの向きがそれだ。電流が逆転すれば、図３から、Ｈは上向きになることがわかる。

　電流を考えているととてもややこしくなるから、直接に電子の動きからすこし考えてみることにしよう。電流のことは時々チェックするときにだけイメージすることにする。太字は総じてベクトル量を表していると、読者の方は解釈願いたい。


２.電線に電流が流れるとき――8/2

われわれはもう電線の中に直接、陽電子と陰電子があって、それぞれが動くときについてイメージしてみる。

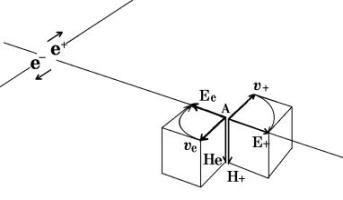図４

電線の両端を電池につないで電圧をかけるとe⁺電子は陰極へ、e⁻電子は陽極へ動こうとするだろう(図４)。(e⁺電子の流れの向きが通常の電流の向きと一致する)。それらは空間にどんな作用をするのかを考えてみる。
　このとき、e⁺が図のような向きに動かされているなら、e⁻はそれとは逆に動くはずだ。また、e⁺が空間の１点Ａにつくる電界はｅ⁺から放射する向きのＥ₊であり、　ｅ⁻のつくるそれはｅ⁻へ向かうＥ_ｅとなる。
　空間Ａに対する陽子ｅ⁺の運動ベクトルは図でυ₊であり、電子ｅ⁻の運動についてはυ_ｅである。するとυ₊についてはυ₊からＥ₊へ回すときにネジの進む向きの磁場Ｈ₊(ベクトル積)が生じるらしい。
　電子のつくっているυ_ｅについては、υ_ｅからＥ_ｅへのベクトル積は図で下向きのＨ_ｅとなる。つまり、空間Ａにｅ⁻流のつくる磁界もｅ⁺流のつくる磁界も同方向である。これは電流のつくる初歩的な理解と一致する。整理しておくと、

３.動く空間では

こんどは見方を変えて、電子たちはじっとしていて、つまり、静電場のなかで、その代わりに空間がマイナスυの速さで動けば、相対的に電子がυの方向に動くのと同義になって、図の向きの磁場が生じるであろうか？

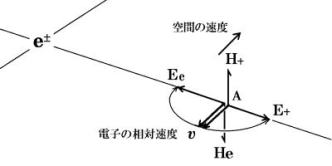　図５

図ではe⁻もe⁺も静止している。そこからＡにある空間で、空間が−υの速度で運動している。このときe⁻のつくる電界はＥ_ｅで、e⁺のつくる電界はＥ₊である。Ａ点は１つであるが、分かりやすいよう便宜的に別けて図示してある。υからＥ_ｅへのベクトル積は下向きのＨ_ｅ、υからＥ₊へのベクトル積は上向きのＨ₊だ。
　e⁻とe⁺が同数であるときはＨ_ｅとＨ₊とは向きが真逆であって、その合成はゼロとなろう。つまり磁界は打ち消しあって存在しないかのようになっている。
　しかし、この図で、

ほんとうにそうだろうか？　このとき、もしもそれと同じ向きの外磁場がかけられていれば、この空間にＨ_ｅによる加速度が生じているだろうか？　すなわち、ニュートリノのような中性の物質が同じくマイナスυの運動をしていれば、その物体の運動方向は曲げられるであろうか？　それを確認することのできる実験は図６のようであろう。

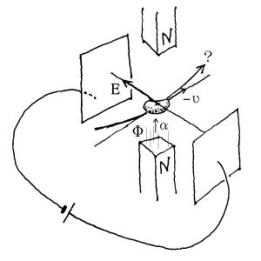図６

遺憾ながら、この実験には大きな装置が必要になると思われるので、とても私的に行なってみることはできない

　さていよいよ「質量は重力場と同一物か？」について言及する段になったが、長くなってお疲れを強いる形になっては申し訳ないので、次号に譲りたい。