8�}�C�P���\���ƃ��[���[�̎����ɂ�����@���������̌����@2
�������u�̊T�v
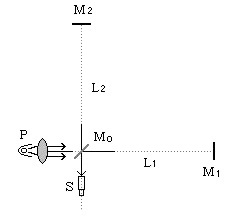
�@����ɕ����ׂĐ����ɒu���ꂽ�l�E�l�i�}�C�P���\���E���[���[�j�̎������u�͐}�̂悤�ŁA45�x�X���Ēu�����X�v���b�^�[�i�n�[�t�~���[�j�̍����ɗႦ�Ό���������B����������˂��ăX�v���b�^�[�Ŕ��˂��ꂽ���͐}�̏���i�n�����]�̔��a�����j�ցA���߂������͉̂E���i���]�����j�֕ʂ�����B
�@���ꂼ��̓A�[����
�@���u�S�̂͌��̍��W�ɑ��E�����]���x���̑����œ����Ă���Ƃ��悤
�@�@�@�@�@�@�@�@�S�̂͐}�̉E�����i�n���̌��]�����j�Ƀ҂̑����œ����Ă�����̂Ƃ���
 |
�X�v���b�^�[�l�O����A�����o�̌����Q���ɕʂ����ďo�����A |
 |
���P�b��Ɍ��]�����̌����l�P�ɓ��B�B�������˂����B ����ɂ��Q�b��Ɍ��]�����̌����X�v���b�^�[�l�O�ɖ߂�A����̌��Əd�Ȃ�A���Ȃ��ώ@����͂��ł���B |
���āA�����O���炔�P�b��ɂ́@���u�͂����P�����E�֓����Ă���B�E�̃~���[�ɓ��B�����Ƃ��X�v���b�^�[�������P�����E�֓����Ă��邩��A�����̌��H�̓A�[����
|
���]���a���������͒x���I |
�}�̂s���͉����ɗv�������ԁB���͂��̊Ԃɂ��̑����Ō��]�����ֈړ����������̔����B![]() �͘r�̒����ł���B���ۂɂ͌��̓W�O�U�O�ɐi�s����B
�͘r�̒����ł���B���ۂɂ͌��̓W�O�U�O�ɐi�s����B
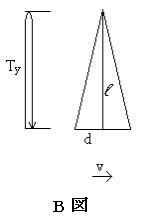 �@�}�̎Εӂɂ����鉝��������S���Ƃ����
�@�}�̎Εӂɂ����鉝��������S���Ƃ����
S�����b�s���@�@�@�@�@�@�@�@�@�@�@�c�c�c�c�c�c�c�c�c�c�@
S�Q�����i�Q![]() �j�Q�{�i�Q���j�Q�@�@�@�@�c�c�c�c�c�c�c�A
�j�Q�{�i�Q���j�Q�@�@�@�@�c�c�c�c�c�c�c�A
�~���[�̓����������Q�������s���@�@�@�c�c�c�c�c�c�B
�s�����P�{���Q�@�@�@�@�c�c�c�c�c�c�c�c�c�c�c�c�c�C
���̐i�s�����͖{��(P.69)�F���̂k��
�k���b�i���P�{���Q�j���b�s�@�@�@�c�c�c�c�c�c�c�c�D
�~���[�̓����������k����
�k�������s�@�@�@�@�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�E
���̏ꍇ�A���]�����������Ԃs�Ɣ��a�����������Ԃs���͕K�������������Ȃ��B��������ƍ��o����ƌ���������ł���B
�{��(P.70)�D������
![]() �@�@�@�c�c�c�c�c�c�c�c�c�c�c�c�F
�@�@�@�c�c�c�c�c�c�c�c�c�c�c�c�F
���ꂩ��e�������Ԕ�s�^�s�����q�������߂Ă݂悤�B�܂��@����
�s����S���^�b
����͇A����
�@��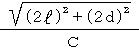 �@�c�c�c�c�c�c�c�c�c�c�c�c�G
�@�c�c�c�c�c�c�c�c�c�c�c�c�G
�B����
��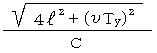 �@�@�@�@�@���b�s����
�@�@�@�@�@���b�s����![]()
���ӂQ�悷��Ɓ@�b�Q�s�Q����![]() ���ꂩ��
���ꂩ��
![]() �@�@�@�@��
�@�@�@�@��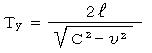 �c�c�c�c�c�c�c�c�H
�c�c�c�c�c�c�c�c�H
����́A�������z�����̃A�[�����������鎞�Ԃ͒P��![]() ���������鎞�Ԃɓ������Ȃ����Ƃ������Ă����I�܂��A���]�����ɉ���������̉������Ԃ́i�{���Ɏ����悤�Ɂj�X�ɒ����B
���������鎞�Ԃɓ������Ȃ����Ƃ������Ă����I�܂��A���]�����ɉ���������̉������Ԃ́i�{���Ɏ����悤�Ɂj�X�ɒ����B
|
���a�����Ɣ�ׂ� |
���z�����������Ԃɑ�����]�����������Ԃ̔䗦�qt�����߂Ă݂悤�B�F�����H���ŏ����B
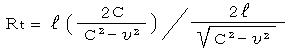
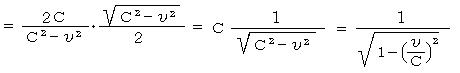
![]() �Ƃ�����
�Ƃ�����
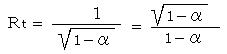 �@�@�@�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�I
�@�@�@�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�I
����͌��]�����̌����������鎞�Ԃ͂���ƒ��p�ȑ��z�����̌����������鎞�Ԃɔ�ׁA���̗��������Ƃ������B
�u���O�̂Ƃ��̂������������Ԃ͇H���ł����O�Ƃ��āA�������͇F������
![]()
�܂�u���O�Ȃ�A��,�������ɕʂ�ĉ����������͓����ɃX�v���b�^�[�֓������邱�Ƃ��Ӗ�����B
��������
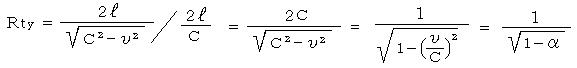
��������
![]()
�����
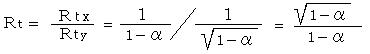 �@�c�c�c�c�c�c�c�c�c�c�c�J
�@�c�c�c�c�c�c�c�c�c�c�c�J
�ƂȂ��ćI���ƈ�v����B
����ǂ͎��ԍ��s�|�s�������߂Ă݂悤�B��������s�Ƃ��āA�F�|�H����
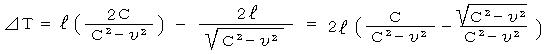
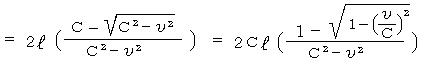
���q����b�Q�ŏ���
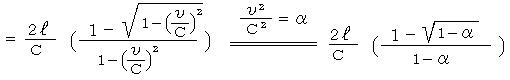
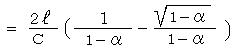 �@�@�@�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�K
�@�@�@�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�K
�G�[�e���_�i�}�C�P���\�������j�ł͂��̑�Q���������Ă��邩������Ȃ��B
|
���̑��Α��x |
�}�C�P���\�����C�Â��Ȃ������͂��͂Ȃ��Ǝv�����A�z�[�L���O�ق��A���ʂɂ͂��̂l�E�l�������u�ŁA���z�Ɍ������Е��̌��͂��̃A�[���ɉ����ĒP�ɉ�������Ɛ�������B�Ȃ��Ȃ�A���]�����ɂ͒n���̌��]���x�œ����Ă��邪�A���z�����ւ͌��]���a�����Ȃ̂ő��z�Ƃ̋����͈�肾�B���͌��]���a�����ւ͂a�}���̂悤�Ɍ��̐�Α��x�ŃA�[���̐���������������邾���Ǝv����B�i�悭�l���Ă݂�ƁA���ۂɂ͂���ȑ��u�̒u�����͓�k�ɒn�ł��Ȃ���Εs�\�Ȃ̂����c�j
��������͌����G�[�e����`���ƍl����Ɗׂ�₷�����o�ł����āA�����������������悤�ɂ݂�������}�̂悤�Ɏ��ۂɂ̓W�O�U�O���s�����邱�Ƃ��ڂ���͒m��B�ŏ��ɂ������}�̒ʂ�ł���B
������A���]���a���������������A�u�n���̌��]���x�̔@���ɂ�����炸�����͈��v�ł͂Ȃ��A���̏ꍇ�����Α��x�b�f�ƂȂ��āA
�b�f��![]()
�ƒx���Ȃ�̂��B������m���߂悤�B
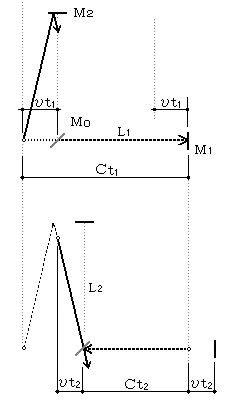
���a�����������A�[����![]() �̃~���[�܂ł̕Г������́A���Α��x�b�f�ł��b�Ԃ����Ăb�f���ł���B���̎��ۂ̑��s�����͎߂ɓ������Ԃ����������b�ő���b���ł���B���̊ԂɃA�[���͌��]�����ւ��������ړ����Ă���B���̊W��
�̃~���[�܂ł̕Г������́A���Α��x�b�f�ł��b�Ԃ����Ăb�f���ł���B���̎��ۂ̑��s�����͎߂ɓ������Ԃ����������b�ő���b���ł���B���̊ԂɃA�[���͌��]�����ւ��������ړ����Ă���B���̊W��
(�b��)�Q�@��(�b�f��)�Q�{(����)�Q
�ł���B���ꂩ��
�b�f�Q���b�Q�|���Q
�ƂȂ邩��A���Α��x�b�f��
�b�f��![]()
�ƂȂ邱�Ƃ�������B����͂܂�
�b�f���b![]()
�Ƃ�������i���P�j�B�����ɗv���鎞�Ԃ͂b�f�����Q![]() ����
����
![]()
����A���]�����̃A�[���ɂ��Ă͖{���̂Ƃ���A�����A�葊�E���ꂽ�����̑��Α��x�͂b�f���b�ł���B
���P�@���̑��x�łs�b�Ԃɐi�ދ����͂b�f�s�ł���B����ȂǂƂ������ȓ���͎g��Ȃ��Ă��o��B���Θ_�ł͌������x���̂łȂ��A�����b�͓����łb�s�f�Ƃ��Ď��Ԃ̂ق����x��A�b�f�s�� �b�s�f���炷��������悤�ɂs�f���s![]() �ƂȂ��Ă���B�l�̓��̒��ɂ����炦���u���ԁv�Ƃ����T�O�̕����I�ɕς��Ă���B���s�������v�Z���Ă݂�Ίm���ɓ��͈�v����B����͍��킹�Ă��邩��A�l�����Ă��������u���Θ_�͊Ԉ���Ă��Ȃ��v�Ǝv�킹��B
�ƂȂ��Ă���B�l�̓��̒��ɂ����炦���u���ԁv�Ƃ����T�O�̕����I�ɕς��Ă���B���s�������v�Z���Ă݂�Ίm���ɓ��͈�v����B����͍��킹�Ă��邩��A�l�����Ă��������u���Θ_�͊Ԉ���Ă��Ȃ��v�Ǝv�킹��B![]() �Ƃ������́A��̃��[�����c�ϊ��ɂ��o�Ă���B�ނ��A�C���V���^�C���̐ꔄ�����ł͂Ȃ��B���Θ_�ł͂b��s�ςƂ������߁A����͎��Ԃ̂ق��ɂ����t���Ă��邱�ƂɂȂ�B
�Ƃ������́A��̃��[�����c�ϊ��ɂ��o�Ă���B�ނ��A�C���V���^�C���̐ꔄ�����ł͂Ȃ��B���Θ_�ł͂b��s�ςƂ������߁A����͎��Ԃ̂ق��ɂ����t���Ă��邱�ƂɂȂ�B
���]���x30�q�^�b�Ƃ��āA���ۂɌv�Z���Ă݂悤
���i�R�~10�^�R�~10�T�j2 =10�|8 ���O�D�O�O�O�O�O�O�O�P
�G�[�e���̕��̒��Ō��]�����̌��̒x��͖{��(P.70)���P�{���Q�@����
![]()
![]() �b�@�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�L
�b�@�c�c�c�c�c�c�c�c�c�c�c�c�c�c�c�L
���̒x��͋����ɂ��ć��w�ł���Ƃ���ƁA
���w![]() �~�b
�~�b
�Q���O�b���Q![]() ����
����![]() �ł���B����������
�ł���B����������
���w���Q![]() �~�@
�~�@![]() �c�c�G�[�e���_�̌v�Z�c�c�c�c�c�c�c�c�@
�c�c�G�[�e���_�̌v�Z�c�c�c�c�c�c�c�c�@
�����̌v�Z�ł́@�K������
���w���Q![]() �~�@
�~�@![]() �c�c�G�[�e���_�̌v�Z�c�c�c�c�c�c�c�c�@
�c�c�G�[�e���_�̌v�Z�c�c�c�c�c�c�c�c�@
�����̌v�Z�ł́@�K������
�������@![]()
![]()
�����ɂ��ć�����
��������t�b���Q�G�[�e���_�i�v���Ⴂ���������Ƃ��āj�Ɣ�ׂ������̌v�Z�ɂ�鋗���̐L�т�
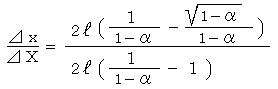
���q����Ɂi�P�|���j������
�@�@�@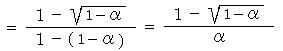
�P�|����0.99999999�����Ă݂��
�@�@�@![]()
�@�@�@��0.000000005�~�P�O�W ���O.�T�O�P�@
�i���z�����ł�����������̒x����l������ƁA�l�E�l���l���锼�����Ó����j
�G�[�e���_�̗\�z�g������S�^10�͎��������ɂ���Ă������菭�Ȃ��ƍl������B�����ɂ��O.�T�قǂɏ��Ȃ߂ɏo�Ă���Ƃ���ƂQ�^10�قǂƂȂ��Ă��邾�낤�B����ɑ��z�����A�[���ɂ������͂��̂������o��0.5��������ƂP�^10�i�P0�^100�j�Ǝ����l�ɋ߂Â��B
���Ȃ݂ɁA��X�̌��H�����v�Z���Ă������B
���H�����K�~�b
![]()
����Ɂ@�P�|����0.99999999�@�����Čv�Z�����![]() ��1���[�g���Ƃ����ꍇ�A100�~10�|�X���Ɠ���B����A���̕W���g����605.8nm��605�~10�|�X���ŁA����ɑ��Č��H����16.5���ɂ�����B
��1���[�g���Ƃ����ꍇ�A100�~10�|�X���Ɠ���B����A���̕W���g����605.8nm��605�~10�|�X���ŁA����ɑ��Č��H����16.5���ɂ�����B
|
�}�C�P���\���̑��Α��x |
�s���āA�}�C�P���\���]���[���[�ɂ��Η\�z���ꂽ�S�^10�g���̂���͂S�^100�ȏ�͔F�߂��Ȃ������ƕ���Ă���i�����ɂ���Ă͑S���F�߂��Ȃ������悤�ɂ��Ȃ��Ă���j�B��X�̖{�����ł͂��̍��͎����덷�ł��낤�ƕЕt�����i�w���q�_�x�o59�j�B�������A����͂��Ȃ��������덷����łȂ��A������x���m�ɔc�����ꂽ���ۂł���Ɛ������邱�Ƃ͏o����B
�}�C�P���\���]���[���[�̊ϑ����S�^100�ȏ�̔g���̂���͌����Ȃ������Ƃ���Ă��邱�Ƃ́A����ɋ߂��Ƃ���܂ł̂��ꂪ�ϑ����ꂽ�Ɖ����邱�Ƃ��ł���B�����ŁA��X�̎��������F���̐���W�ɑ��Ă����Ȃ鑬�x�������͊F�ڕs���ł��邪�A���̐���W�ɑ��ĂȂ�炩�̑��x�ł������Ƃ���A���̑��x�ɑ��Ăl�E�l�̑��u�́A���o����Ȃ�45�K���邢�͖ʂɑ���90�K�Ƃ͌��炸�A�l�X�ȌX���Ȃ��Ċϑ������̂ł͂Ȃ����낤���B
���]���x�̌����ɍ��킹������̂l�E�l�̑��u�����̐���W�̌X���ɑ��Ď��X���X�O�K����90�K�܂ł̂���X�������ĉ^������r�����ϑ������͂��ŁA���̑��Α��x�ɑ�������g���̂���͂��̂O����100�p�[�Z���g�܂ň�����l���ϑ����邾�낤�B
���]�����ɍ��킹������̃A�[���ɉ����Đ^�̉^�������������������̑��Α��x�ɑ��A����ƒ��p�ȃA�[���̕��ɂ����Α��x�������A����痼���̍����g���̂���Ƃ��Ċϑ�����Ă���͂����B�܂�A�ϑ��l�͎v������肳��ɏ����߂Ɍ��o����Ă������ƂɂȂ�B
�}�C�P���\���]���[���[���ϑ������g���̂S�^100�̂���ɑ������鑊�Α��x���v�Z����A���̒n���̐��Ԃɑ���^�����x�́A���Ȃ��Ƃ������葬�����Ƃ͊m�F�ł��邱�ƂɂȂ낤�B�t
|
�n���̐�Α��x�����߂� |
�}�C�P���\���]���[���[�̕ŁA�S�^10�g���̂���Ɨ\�������ϑ����ʂ͂���10����1�ȉ��ł������Ƃ��Ă���B���z�ƒn���̊W�𗧑̓I�ɃC���[�W���Ă݂悤�B���z�����A�[���z�Ɍ����Ă��A���]�����̃A�[���́A���u���̂���ɒn�ʂɐ����ł��邽�ߒ��Ɨ[�ɂ͑��z�����ƕ��s�ɂȂ��Č��]�������w���Ȃ��B�A�[�������]�����̑��x��100�p�[�Z���g������̂͐��߂��[��0���ł���B�����Ɋ|���鎞�Ԃ͒��H���Ƃ鐳�߂����Ԃ���������낤�B�ߑO���ɏI���悤�Ƃ���A�o�����Ɏ��|���邱�Ƃ��K�v���B���킽���������Ԃ�����A���������ăf�[�^���Ƃ낤�Ƃ���A���x�݂̂̂����u�̏����ɂ����邾�낤�B�ŏI�f�[�^���L�^����鍠�͂����炭3���ȍ~�ŁA���߂�����������Ǝ��|�������Ƃ���ƁA�����Ȃ�ƂȂ�̂͗[���������낤�B��������ƁA���]�����ɑ��Ă��S�������ϑ�����Ȃ������Ƃ������ƂɂȂ�B�ނ炪�ϑ������u�S�p�[�Z���g�܂łɉ߂��Ȃ��Y���v�͓��Ă����ƌ����ׂ����B
�܂��^���Ɛ[��̊Ԃɂ��A�n���̎��]���x�����ꂼ��t�ɑ��������B���]���x�ƍl�������x���A��͂̒��S�ɑ��鑾�z�̌��]���x���n���̌��]���x�ɉ�������A���܂��ܑł������������ł������ꍇ�́A���Ǝv���Ă������]���x�����܂�Ŗ����̂�������Ȃ����A���]���x�Ǝv������葬����������Ȃ��B�������A���̋�͌n�����A���Ԃ̂ǂ̌����ւǂ�قǂ̑����œ����Ă��邩�͕s���ł���B
���̂悤�ɂ��đ��������E����Ă����ƁA�����̂l�E�l���u�̐��Ԃɑ��鑬���͑��O�A�ނ炪�ϑ������A�g���̍ő傸��Ɋ��Z����100����4�̂�����x�ł���̂����m��Ȃ��B
�}�C�P���\���������\������10����4�̔g������́A����0.5�قǂ��������͂��������Ƃ����100����20�̂��ꂪ�ϑ������͂��ł��邪�A�����������O����100�p�[�Z���g�܂ł̒��Ԃł���Ƃ����100����10�̂��ꂪ������ׂ��Ƃ���A100����4�ȉ��ł������Ƃ�������A�F���^���̑��E�ɂ���Ă��̒l�܂ʼn��������Ƃ��l������B
���邢�́A�������I������̂��ǂ����Ă��[���ɂȂ����Ƃ����10�̂͂����S�ɂȂ肳��Ƀ[���܂ʼn\��������B������ɂ���A���̑��Α��x�͊ϑ��l�ɕ\�ꂽ�Ƃ�����B���������āA�����l�E�l���u�ɂ���Ēn���̐�Α��x�����߂悤�Ƃ���Ȃ�A�n����̖k�ɂ����ɂ܂ŁA�ܓx�ɂ��Ă�0�x����180�x�܂ł̈ʒu�ɑ����̎����ݔ���z�u���āA�������Ɉ�ĂɊϑ�����K�v������B���̒��ōő�̒l���Ƃ������̂������炭�n���̂��̎����ɂ������Α��x�ł���B�Ȃ��Z�p���C�^�[�E�c�o�i���ɂ��A���[�U�[�W���C���͎��Ȃ̉^�����x�������Ƃ����B