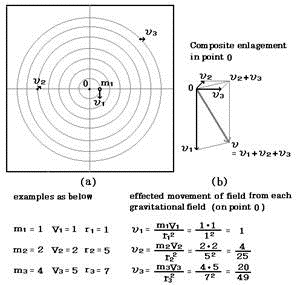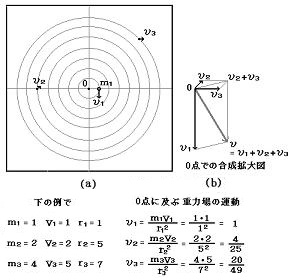
第３図
第2図にある天体ｍ３を例にとりますと、Ｏ点から距離7ｒ1にある質点ｍ３のつくる重力場がＯ点に及ぼす重力場の強さは、ニュートンの万有引力の法則から、ｍ１のそれに比べ１／（7ｒ1）２になるでありましょう。質量ｍ３がｍ１の４倍だとしますと、その運動速度Ｖ３がＯ点に及ぼしている影響はＶ３×4ｍ１／（7r1）2となると考え、この値をυ３とします。
これはｍ１による重力場運動に対し、どれほどの比になるかをみますと、まずｍ１がＯ点に及ぼす速さは、さきのような計算で、υ１＝Ｖ１×ｍ１／ｒ1２ということになります。
つぎに、さっきのＶ３がｍ１のもつ速さＶ１の５倍あるとしますと、υ３は
υ３＝５Ｖ１×４ｍ１／（7ｒ1）２
と表わせます。υ１に対する絶対値の比をとってみますと
υ３／υ１
＝［5V1×4m1/(7 r1) 2］／［V1×m1/r12］
従ってυ３をυ１で表わしますと
υ３＝［5×4×ｒ1２／（7ｒ1）２］υ１
＝［5×4／49］υ１
となります。第3図、下の表でυ１＝１×υ１としますと、υ３は
υ３＝（20／49）υ１です。
ｍ２を例にとっても、同様の考えから、そのυ２はυ２＝(4/25)υ１と得られます。
各天体からO点に及ぶ重力場の運動速度υ１、υ２、υ３をO点で合成するには、第3(b)図に示すベクトル合成によります。
これは第2図のＶ１と同じであるはずのものを、
...............Fig.3
The table under it shows the calculations for this example, and
the right-hand figure (b) is expanded and shows that composition. As for the celestial body m3 in Fig.2, for example, the strength of the
gravitational-field (which reaches from the gravity source point m3 in the distance
7r1 from O) by m3,
will be set to 1/(7 r1)2 according to Newton’s Law of
gravitation, compared with that of m1. When
mass m3 is 4 times m1, the influence
which its movement speed V3 exerts on
point O will be set to V3×4m1/ (7 r1)2. Let's
set this value to υ3.
How much ratio has υ３ for the movement of gravitational-field
resulting from m1? The speed which m1 exerts on point O,
as in the above calculations, is set toυ1=V1×m1/r12.
Next, supposing
above V3 has 5 times of the speed V1 which m1
has, then υ3 will be expressed as
υ3=5V1×4m1/(7 r1)
2.
The ratio of an absolute value
toυ１is,
υ3／υ1
＝［5V1×4m1/(7 r1) 2］／［V1×m1/r12］ Therefore, υ3 is
denoted byυ1,
υ3＝［5×4／49］υ1
If [ in the table under fig.3 ]
let
υ1＝1×υ1, then
υ3= (20/49)υ1
Similarly, for example m2,
theυ2 will
be obtained withυ2=(4/25)
υ1
The composing calculation of the movement speeds υ1,υ2, andυ３ of the gravitational-fields
which range from each celestial body to point O, are made by method shown in Fig.
3(b).
In order to make it legible, it shows the same one
as V1 of Fig.2 is expanded to length ofυ1
in Fig.3(a)