埨堈偵尵偊傫偱偟傚偆側丅偲偵偐偔丄抧媴奺晹偵媦傇彮側偔偲傕丄寧偵嬤偄懁偺寧偵懳偡傞墦怱椡偼寧偐傜墦偄懁偵斾傋彫偝偄偙偲偼尵偊傑偡丅偮傑傝丄抧媴帺揮偼寧偵懳偡傞墦怱椡傪抧媴忋偺寧偵嬤偄懁偱偼彫偝偔丄寧偐傜墦偄懁偱偼戝偒偔偝偣傞丄偲尵偭偰傕傛偄偐傕偟傟傑偣傫丅
丂偪側傒偵丄帺揮妏懍搙冎倕偺丄岞揮妏懍搙冎偵懳偡傞斾丄傪尒偰傒傑偡偲丄[俀兾乛擔]懳[0.23乛擔]亖栺俀俈偮傑傝丄抧媴帺揮妏懍搙偼岞揮妏懍搙偺栺俀俈攞偁傞傢偗偱偡丅
拹仸丂偙偺偙偲偼偳偺晹暘偱傕惉傝棫偭偰偄傞偐傜丄偨偲偊岞揮拞怱偑抧媴撪晹偵偁偭偨偲偟偰傕惉傝棫偮丅幚偺偲偙傠俼侽偼4.66亊10俁噏乮戞侾侾榖俀偐傜乯偱偁傞偑丄抧媴偺敿宎倰偼栺6.3亊103噏偱俼侽傛傝戝偒偔丄岞揮拞怱偼抧媴偺撪晹偵偁傞丅側偍丄岝偑抧媴傪侾昩娫偵俈.俆廃偡傞偙偲偐傜媮傔傞偲丄抧媴敿宎倰偼倰亖6.3亊103噏丂偲側傞丅
俀丂抧媴帺揮偵娭偡傞峏側傞専摙
丂乗乗偝偭偒偺乽抧媴帺揮妏懍搙偼岞揮妏懍搙偺栺俀俈攞乿偱偁傞偙偲偼柍帇偱偒側偄偱偁傝傑偟傚偆丅濨枂偺傑傑偵偟側偄偱妋擣偟偰傒傞偙偲偵丄彅孨丄堎懚偼側偄偱偟傚偆側丅壖偵帺揮妏懍搙偑岞揮妏懍搙偵摍偟偄応崌偲丄侾俀攞偱偁傞応崌偲傪恾偵昞傢偟偰傒傞偲丄抧媴忋偺侾揰倣侾偍傛傃倣俀偼恾偺傛偆側婳愓傪昤偔偱偟傚偆丅恾偺撪墌偼抧媴岞揮偺撪愙墌丄奜墌偼抧媴岞揮偺奜愙墌偱偁傝傑偡丅撪墌偵愙偡傞弖娫偺抧忋偺偳偺揰傕丄摨偠宍偺婳愓傪昤偒傑偟傚偆丅 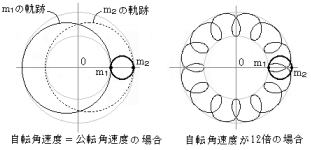
恾俁丂丂 |
|
偡側傢偪丄寧偵嬤偄偳偺揰傕彫偝偄屖傪昤偒丄墦偄偳偺揰傕戝偒偄屖傪昤偔傢偗偱偡丅彅孨偼偙偺恾偐傜丄彫偝偄屖偼岞揮墦怱椡傪徚幐偝偣丄戝偒偄屖偼彆挿偡傞偙偲傪娤嶡偡傞偙偲偑偱偒傑偟傚偆丠丂岞揮墦怱椡傪徚幐偝偣偨暘丄寧偺堷椡偑嬓傪棙偐偣傞偙偲偵側傞傢偗偱偡丅
丂墦怱椡偺庛偄傎偆偼嫮偔寧偵堷偐傟丄嫮偄傎偆偼寧偐傜傕墦偞偐傠偆偲偡傞偱偟傚偆丅側偍丄幚嵺偺抧媴偼侾俀屄偱側偔丄栺俀俈屄偺僒僀僋儘僀僪傪昤偔偼偢偱偡丅丂乗乗偝偭偒彫惗偼丄帺揮妏懍搙偑岞揮妏懍搙偵摍偟偗傟偽嘆嘇幃偼惓偟偔揔梡偝傟丄兛俙亙兛俛偱偁傞偲尵偭偨偐偲巚偄傑偡丅偦偺嵎堎偼丂乽亅倰冎俀乿偲乽亄倰冎俀乿偺嵎偲偄偆偙偲偵側傝傑偡丅奺晹偵媦傇抧媴帺恎偺廳椡応偵偮偄偰偼丄惷巭帪偺抧懴椡偲掁崌偭偰姰寢偟偰偄傞偼偢偱偡丅丂4恾偱偼丄幚嵺偵懄偟偰岞揮拞怱俷偑抧媴撪晹偵偲偭偰偁傝傑偡丅塃曽岦傪亄偲偟傑偟傚偆丅岞揮妏懍搙傪冎丄帺揮妏懍搙傪冎倕偲偡傟偽幙揰倣侾偵偐偐傞
丂丂堷椡偼丂丂亅俧俵乛(俼亅倰) 俀
丂丂岞揮墦怱椡*偼丂亄俼侽冎俀
丂丂帺揮墦怱椡偼丂亅倰冎倕俀
丂偟偨偑偭偰倣侾偵偐偐傞壛懍搙兛侾偼丄偙傟傜偺崌寁丂兛侾
亖亅俧俵乛(俼亅倰) 俀亄俼侽冎俀亅倰冎倕俀丂乧嘊
偱偁傝傑偟傚偆丅側偍丄慜偵傒偨傛偆偵岞揮墦怱椡偼偳偺晹暘傕摍偟偄偱偡丅丂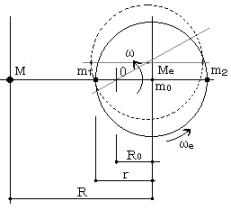 丂恾係 丂恾係
|