弧m,nはそれぞれP1, P2を通る経線を示します。図4はその断面図です。
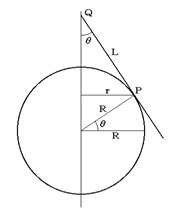 図4 図4
その図から見るとおり、Pの回転半径はrです。すると、弧がmからn まで移動するまでにPの動いた距離、弧P1P2つまり弧dは
d=rω0 ……………①
点P1において水平面での経線の延長はいずれ地軸と交わります。その交点をQとしますと、P2での経線延長もまたQを通ることになりましょう。P1の経線延長とP2の経線延長とはQ点で交わり、その角度だけその間に傾斜してきたわけです。その間のP地点での回転角度がその角度にほかなりません。
その角度をψラジアンとしますと、弧dはその角度にLを乗じたものとして得られましょう。すなわち d=Lψあるいはψ=d/L……②
の関係です。Lとrは図からLsinθ=r であって L=r/sinθ ……………③
すると1秒当りのψは②,①および③から
ψ=d/L=rω0/(r/sinθ)
=ω0 sinθ ………………④
すなわち、緯度θにおける地面の回転角速度ωは地球の自転角速度にsinθを乗じた角速度 ω=ω0 sinθ
として持つことがわかるでしょう。
|
|
赤道上ではθ=0であり、地面の回転はゼロですが、極地Nではθ=π/2となって、地面は地球の自転と同じω0の角速度で回転していることがわかります。
なお、物理学では角速度ベクトルを回転軸と平行な、つまり回転面と垂直な矢の向きと長さ(回転速さ)で表すことになっています。このベクトル表示による合成・分解の結果はもちろんベクトル計算法の結果に適合することがわかっています。
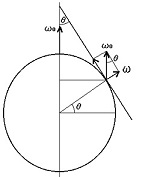 図5 図5
その算法によっても、緯度θにおける地面に平行な自転角速度ωは図5から
ω=ω0 sinθ
と求められます。
MGP実験が示したものは
図は先に説明した装置を模式的に示したものです。実験地での地球自転による地面の回転角速度はωだとしましょう。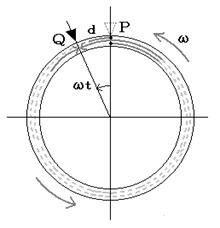 図6 図6
|